Astrocartografía del vector armonico

1. El vector armónico 

       El concepto de Vector Armónico fue introducido por Miguel García en varios de sus trabajos durante los años 1991 al 1997. Hacemos especial mención de llamado “Una Formulación Matemática de los Harmogramas y de la Fuerza de los Números en las Cartas Astrales”. 

Para dar una idea intuitiva, diremos que el Vector Armónico de propuesto por Miguel García está íntimamente relacionado con la Resultante Planetaria de A.Boudineau y que ésta, a su vez, puede considerarse como una respuesta al desafío de cómo calcular el punto medio de todos los planetas de una carta; más concretamente, es el producto de una suma de vectores, cada uno de los cuales representa la longitud eclíptica de un planeta en una carta astral determinada. 

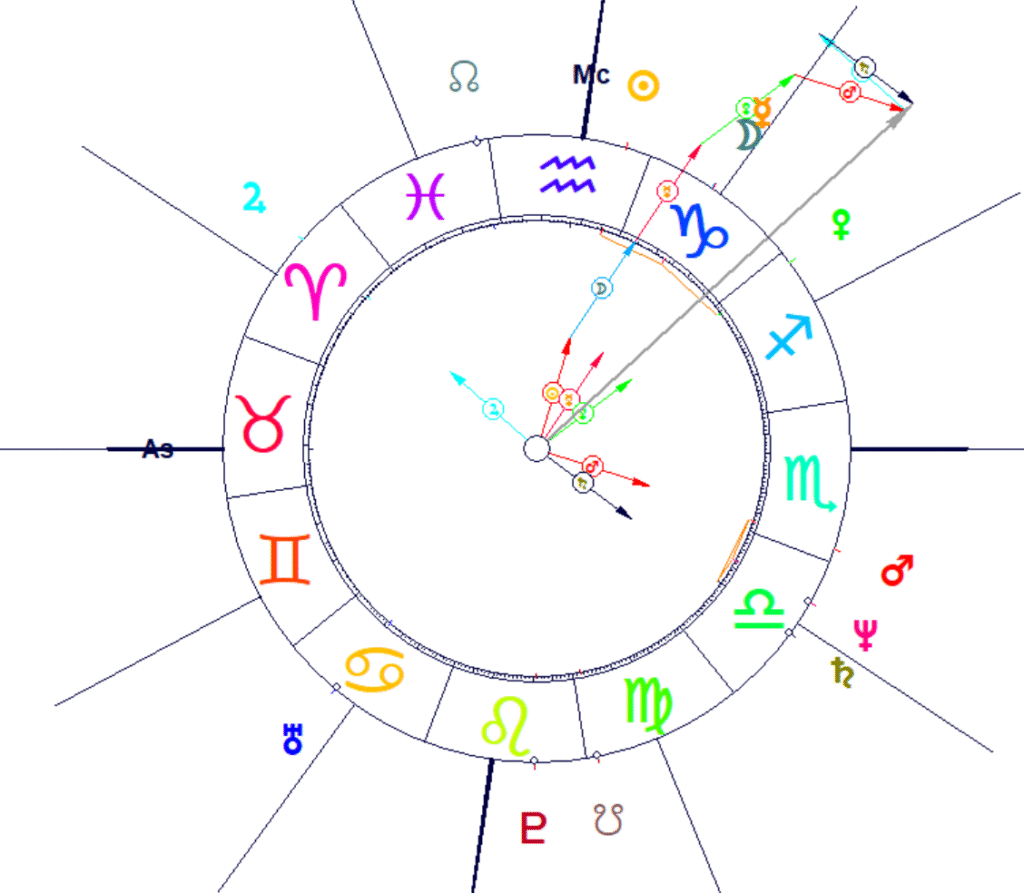
Podemos imaginar la Resultante Planetaria como el lugar donde converge un conjunto de fuerzas cósmicas en conflicto, cada una de las cuales tira de la Tierra en una dirección diferente, pero todas con la misma intensidad. Señala, pues, el lugar del zodiaco donde se concentra toda la energía planetaria en un solo punto. En este caso para el armónico 1 es el 2° capricornio aproximadamente.

El vector suma de todos los planetas es la Resultante Planetaria de Boudineau (RPB). Este vector resultante apuntará a un grado del zodíaco, que es el que se puede considerar el punto medio de todos los planetas; pero, además de señalar ese importante punto de equilibrio o concentración de fuerzas, la suma de vectores proporciona información sobre la intensidad alcanzada por ese punto, la cual no es ni mucho menos la misma en todas las cartas. Esta intensidad está en proporción directa a la longitud del vector resultante.

       El Vector Armónico de M.García extiende la aplicación de la RPB a todos los armónicos, entendidos éstos como ondas sinusoidales puras de amplitud 1 y frecuencia h (donde h es el número del armónico). 

Hasta aquí hemos explicado cómo se obtiene la RPB del armónico 1 de cualquier carta. Para obtener la RPB de otro armónico cualquiera, se calcula primero la carta de ese otro armónico y luego se procede igual que si se tratase del primer armónico. Por ejemplo, para la misma carta anterior, pero en armónico 2, el punto de mayor amplitud es en el 19° Libra

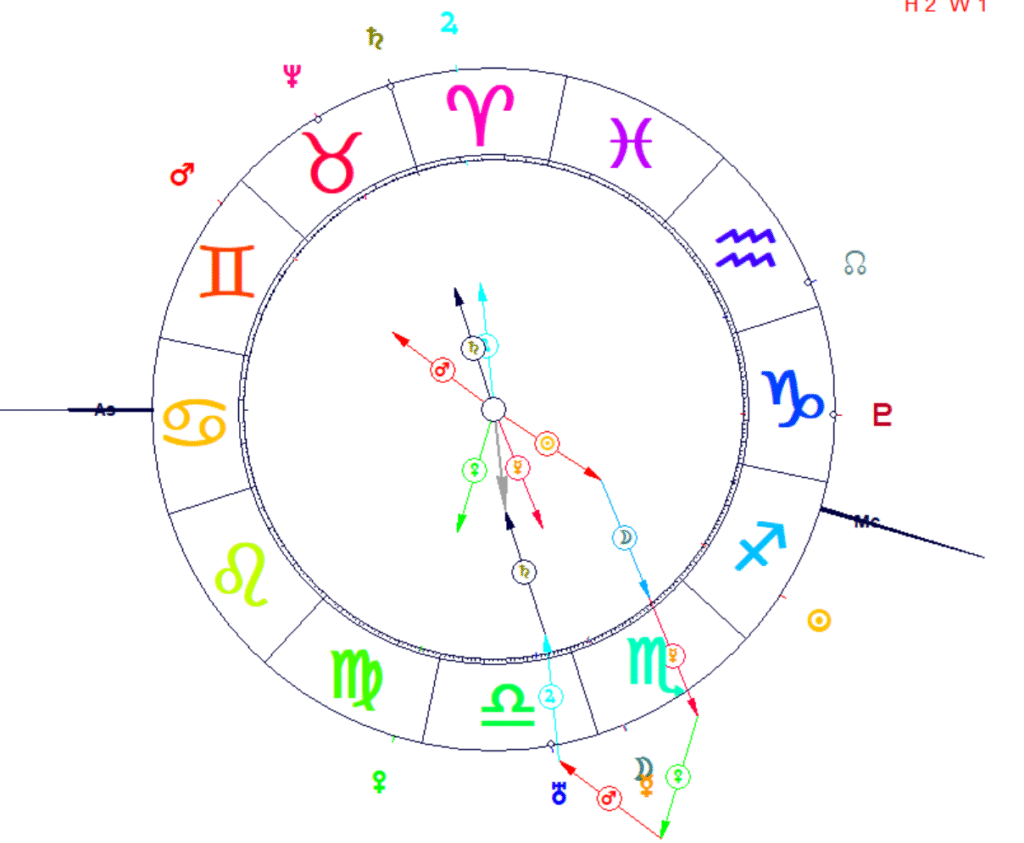
Estos cálculos constituyen la base de la Flor Armónica. Esta última es un recurso gráfico que representa simultáneamente la incidencia en el zodiaco de varios vectores armónicos correspondientes a las posiciones eclípticas de los planetas en las primeras 12 cartas armónicas, desplegados en tantos brazos (pétalos) equidistantes entre sí como sea el número del armónico. 

2. Dificultades teóricas que entraña la noción de vector armónico. 

       Al margen de la complicación matemática de su cálculo, el vector armónico plantea dos problemas. El primero es a partir de qué planetas debemos calcularlo. El segundo, si está realmente justificado dar el mismo peso (matemático) a todos los planetas. 

En realidad, los dos problemas están íntimamente relacionados, pues si como respuesta al primero decidimos que hemos de dejar fuera, por ejemplo, los asteroides, Quirón y los planetas exteriores, incluyendo tan sólo los siete planetas tradicionales

(esta selección es la que viene «por defecto» en el programa Armón). eso es tanto como admitir que no todo planeta merece la misma consideración ni, por consiguiente, el mismo peso en el cálculo. De esta manera, habríamos clasificado los planetas en dos grupos: 

       a) planetas de peso 1 (los 7 clásicos) 

       b) planetas de peso 0 (todos los demás) 

Sin embargo, esta solución de tipo todo o nada parece demasiado drástica y tiene como resultado, entre otras cosas, equiparar la potencia de mercurio con la del sol. Después de todo, una selección como la que ilustramos parece no tener más fundamento que la costumbre, junto con vagas consideraciones acerca del tamaño, la distancia, la luminosidad y el estar esos planetas al alcance de la vista en condiciones de observación favorables.

La costumbre no constituye por sí misma ningún argumento de validez científica; en cuanto al tamaño, en términos absolutos urano y neptuno son mayores que mercurio, venus, marte o la luna; y el sol es mucho mayor que todos los planetas juntos. Además, hay estrellas mucho mayores que el sol. En términos relativos (tamaño aparente en función de la distancia) el sol y la luna por sí solos deberían completar la selección. 

Si ponemos el énfasis en la distancia, forzoso sería incluir el cinturón de asteroides completo, además de los satélites de marte, júpiter o saturno. En cuanto a luminosidad, el sol barre de nuevo; además, habría que incluir las estrellas y los cometas y excluir a mercurio cuando no es visible. Y también habría que hacer esto último en relación al criterio de «perceptibilidad a simple vista». Como se ve por todo lo anterior, hacer una selección coherente de planetas no es tan sencillo; sin contar con la presumible intervención de todos los cuerpos celestes que todavía quedan por descubrir.

El segundo problema puede eludir más fácilmente subrayando el carácter armónico del vector. Esto significa que no estamos tratando estrictamente con características materiales de los planetas, ni tampoco con la fuerza expresiva de los contenidos simbólicos que se les asocian. Tratamos nada más que con ángulos (que a su vez expresan ondas); y así como a la hora de calcular un punto medio entre dos planetas no les asignamos pesos relativos a cada uno, tampoco tenemos que hacerlo al buscar un punto matemático de equilibrio angular entre tres o más cuerpos.

Puede parecer un problema añadido que ciertas configuraciones planetarias pueden dar un RPB de longitud cero que no apunta a ninguna parte. Tal es el caso, por ejemplo, de un Gran Trígono (tres planetas, a intervalos de 120 grados) o de una Gran Cruz Cósmica (cuatro planetas a intervalos de 90 grados) y, en general, de cualquier distribución de n planetas que divida al zodíaco en n partes iguales. Pero esto no es un problema, sino una propiedad de la suma de vectores, ya que, en estos casos, la RPB apunta al centro de la carta. Esto, a su vez, significa que el armónico 1 (es decir, su onda asociada) es muy débil, pero, a cambio, el armónico n será sumamente poderoso. Y esto no escapa al vector armónico propiamente dicho, que recoge la suma de todos los armónicos.

        Ante todas estas dificultades teóricas se puede reaccionar de muy diversas maneras. Quizás las tres salidas más típicas serían:

        1) Efectuar una selección de planetas, ignorando todas las objeciones, al amparo del dicho «creo que esta es la selección correcta, porque lo siento así».

        2) Darse por vencido y renunciar a trabajar con el vector armónico.

      3) Ensayar distintas alternativas y observar su rendimiento para ver «cuál es la buena».

Pero cualquiera de estas soluciones parece viciada por la inclinación a creer que hay un vector armónico absoluto y sólo uno. Una solución más pragmática consiste en emplear la expresión vector armónico asociada en cada caso con una mención explícita de la selección efectuada. 

Nada nos impide hablar del «vector armónico de n planetas», en lugar de «vector armónico» a secas, siempre que especifiquemos la lista completa de planetas incluidos. Dicho de otra manera, si nadie ve un problema en el hecho de trabajar con el punto medio de sólo dos planetas, tampoco tiene por qué haberlo en usar algo así como el punto medio de, por ejemplo, sólo siete planetas. 

El RB es un punto que aglutina siete planetas debe ser interpretado como integrando los significados de todos y cada uno de esos siete planetas en relación al punto donde convergen. 

En cualquier caso, siempre indicará un punto sensible capaz de movilizar a todos los planetas implicados cuando sea activado por un tránsito o alguna otra forma de dirección.

3.- Astrocartografía de vectores armónicos

Establecido esto, podemos pasar a mostrar alguna aplicación práctica de los vectores armónicos. 

Más concretamente, vamos a analizar qué puede aportar esta técnica al esclarecimiento de los condicionamientos astrológicos que pudieron intervenir en el terremoto mas grande de la historia registrado.

El terremoto más grande registrado en la historia fue el Gran Terremoto de Chile o Terremoto de Valdivia, que ocurrió el 22 de mayo de 1960.

Tuvo una magnitud de 9.5 en la escala de momento sísmico (Mw​), la cual mide la energía liberada por un sismo. La ruptura de la falla abarcó aproximadamente 1.000 kilómetros.

Este evento fue tan poderoso que no solo causó una gran devastación en Chile, sino que también generó un tsunami que viajó a través del océano Pacífico, afectando a lugares tan lejanos como Hawái y Japón.

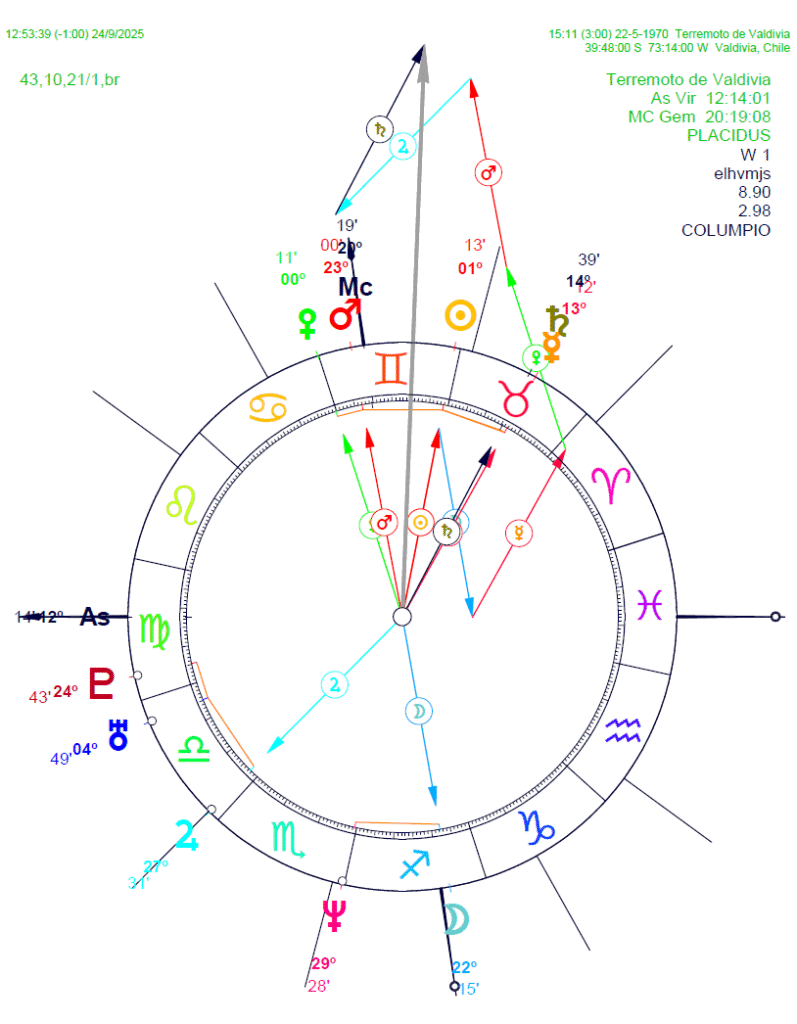
De las tres preguntas que un estudio completo debiera tratar de responder -por qué sucedió eso, por qué sucedió entonces y por qué sucedió ahí- nos concentraremos tan sólo en la última, aunque también diremos algo de las otras dos. Pero para poder ensayar una respuesta a esta última, nos vemos precisados a combinar la técnica de los vectores armónicos con la astrocartografía.

        De la misma manera que podemos ubicar un planeta sobre un mapa terrestre, podemos también localizar en ese mismo mapa el punto medio entre dos planetas. Y si podemos hacerlo con un punto medio, ninguna dificultad habrá en hacer lo mismo con un vector. De esta manera, el vector (RPB) señalará un lugar de la superficie terrestre que, al menos en teoría, recoge la máxima presión procedente de todos los planetas usados para el cálculo de ese vector. En este caso el vector armónico se ubica en el grado 9°41´de Géminis

Esta dirección puede registrarse con las técnicas de la astrocartografía, y el programa Armon  nos suministra para ello gráficos sumamente expresivos. 

El epicentro del Gran Terremoto de Chile de 1960 se localizó frente a las costas de la ciudad de Valdivia.

Las coordenadas exactas varían ligeramente según la fuente y los estudios posteriores, pero generalmente se citan alrededor de:

• 38° 08′ 35″ Sur
• 73° 24′ 25″ Oeste

El hipocentro (el punto de origen del sismo en el interior de la Tierra) se ubicó a una profundidad de aproximadamente 35 a 60 kilómetros. Es importante notar que, debido a la enorme extensión de la ruptura de la falla (cerca de 1,000 km), el terremoto no fue un solo punto, sino un evento masivo que se propagó a lo largo de la zona de subducción entre la Placa de Nazca y la Placa Sudamericana.

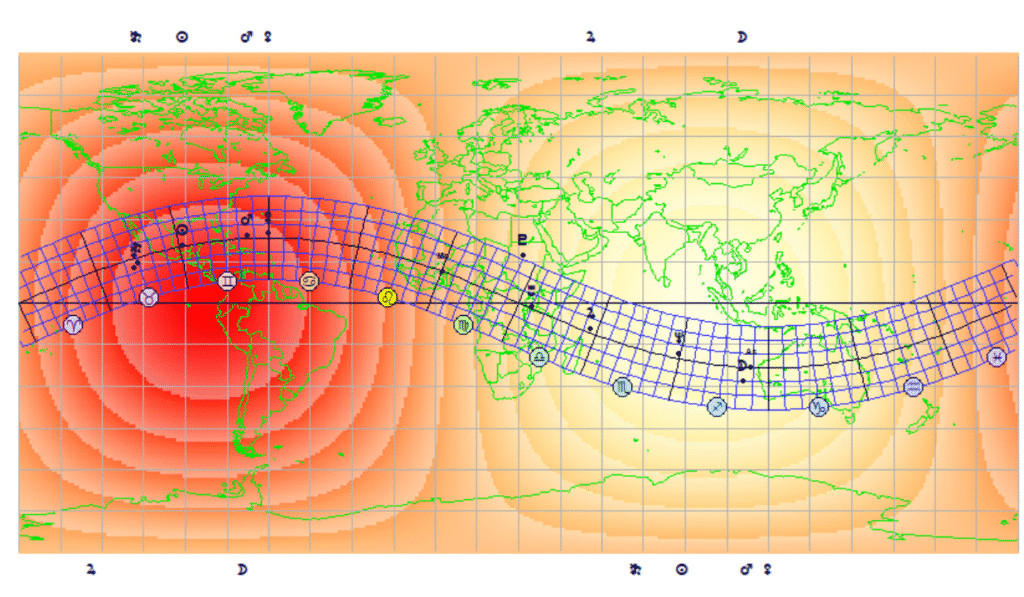
No es fácil percibir los detalles geográficos ni los símbolos en una imagen del tamaño que muestra el programa. Para ver con más claridad a qué distancia del epicentro se sitúa el vector armónico es conveniente ampliarla.

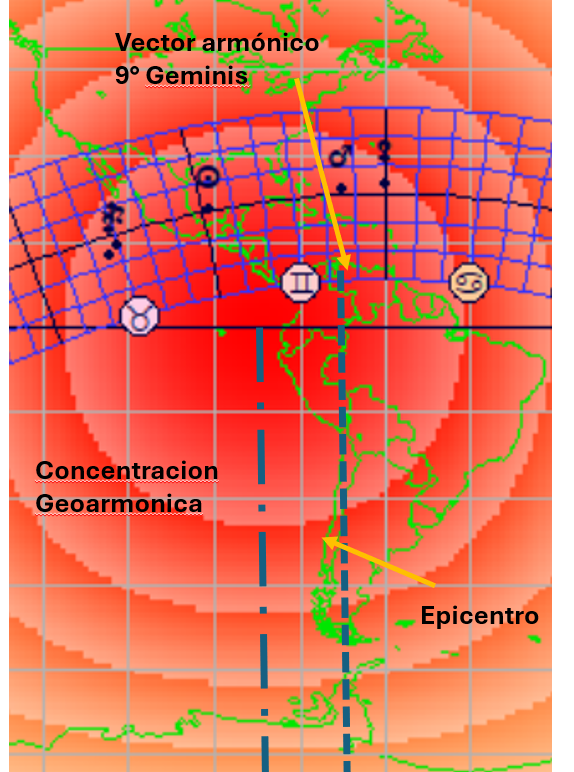
Ahora podemos ver que el vector armónico se encuentra a una distancia del epicentro que, traducida a tiempo, representa aproximadamente menos de una hora. Es decir, que el vector armónico se demoraría aún ese tiempo en llegar al epicentro, después de desencadenado el suceso. Y continuaría después girando en torno a la Tierra hasta completar una vuelta en unas 23 horas más. El vector armónico es, pues, un factor de desplazamiento rápido, demasiado rápido, diría yo, y apuntando a demasiados lugares en poco tiempo como para poder achacarle efectos tan desproporcionados. 

Sin embargo, las conexiones siguen siendo muy débiles. El vector armónico barre todos los días tanto la zona siniestrada como el perímetro entero del planeta, en las proximidades del ecuador. Sería necesario disponer de alguna técnica que fijara el vector armónico en una zona bien determinada de la Tierra durante un periodo suficientemente amplio para que llegue a ser significativo en relación con cualquier cosa que en ese lugar pueda llegar a suceder.

La astrología no nos deja sin recursos a este respecto. Nos brinda toda una serie de cartas que pueden cumplir esta función: las grandes conjunciones o configuraciones universales, los eclipses, las lunaciones y los ingresos del Sol en Aries, figuran entre las más significativas.